北师大版(2012)数学八年级上册《勾股定理》PPT课件(第2课时)
展开
《勾股定理》PPT课件(第2课时)
第一部分内容:学 习 目 标
会运用勾股定理求线段长及解决简单的实际问题. (重点)
能从实际问题中抽象出勾股定理的数学模型,并能利用勾股定理建立已知边与未知边长度之间的联系,进一步求出未知边长. (难点)
新课导入
知识回顾
勾股定理:直角三角形两直角边的平方和等于斜边的平方.
几何语言:
∵在Rt△ABC中 ,∠C=90°,
∴a2+b2=c2(勾股定理).
勾股定理揭示了直角三角形三边之间的关系.
... ... ...
勾股定理PPT,第二部分内容:知识讲解
勾股定理的简单实际应用
问题1: 一个门框的尺寸如图所示,一块长3m,宽2.2m的长方形薄木板能否从门框内通过?为什么?
分析:可以看出木板无论横着,还是竖着都不能通过,所以只能考虑斜着.观察可以发现 AC的长度是斜着能通过的最大长度,所以只要AC的长大于木板的宽就能通过.
问题2:如图,一架2.6m长的梯子AB斜靠在一竖直的墙AO上,这时AO为2.4m. 如果梯子的顶端A沿墙下滑0.5m,那么梯子底端B也外移0.5m吗?
归纳总结
利用勾股定理解决实际问题的一般步骤:
(1)读懂题意,分析已知、未知间的关系;
(2)构造直角三角形;
(3)利用勾股定理等列方程;
(4)解决实际问题.
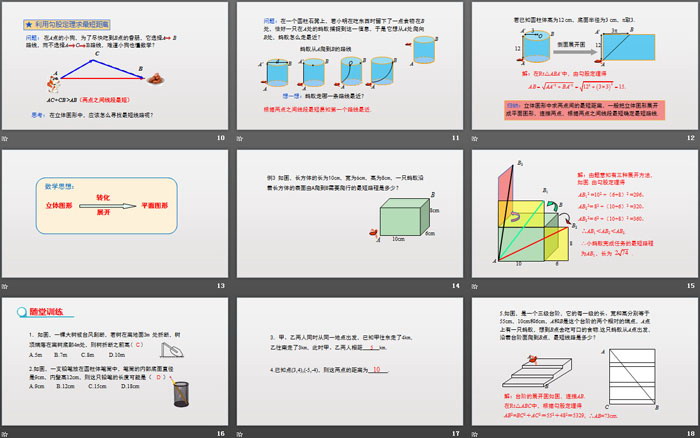
例1 如图,有两棵树,一棵高8米,另一棵2米,两棵对相距8米.一只鸟从一棵树的树梢飞到另一棵的树梢,问小鸟至少飞行多少?
利用勾股定理求两点间距离
例2 如图,在平面直角坐标系中有两点A(-3,5),B(1,2)求A,B两点间的距离.
... ... ...
勾股定理PPT,第三部分内容:随堂训练
1.如图,一棵大树被台风刮断,若树在离地面3m 处折断,树顶端落在离树底部4m处,则树折断之前高( )
A.5m B.7m C.8m D.10m
2.如图,一支铅笔放在圆柱体笔筒中,笔筒的内部底面直径是9cm,内壁高12cm,则这只铅笔的长度可能是( )
A.9cm B.12cm C.15cm D.18cm
3.甲、乙两人同时从同一地点出发,已知甲往东走了4km,乙往南走了3km,此时甲、乙两人相距______km.
4.已知点(3,4),(-5,-4),则这两点的距离为_______.
5.如图,是一个三级台阶,它的每一级的长、宽和高分别等于55cm,10cm和6cm,A和B是这个台阶的两个相对的端点,A点上有一只蚂蚁,想到B点去吃可口的食物.这只蚂蚁从A点出发,沿着台阶面爬到B点,最短线路是多少?
... ... ...
勾股定理PPT,第四部分内容:课堂小结
利用勾股定理解决实际问题
利用勾股定理求两点间的距离
利用勾股定理求最短距离
关键词:人教版八年级下册数学PPT课件免费下载,勾股定理PPT下载,.PPT格式;