《函数的奇偶性》函数的概念与性质PPT(第1课时函数奇偶性的概念)

《函数的奇偶性》函数的概念与性质PPT(第1课时函数奇偶性的概念) 第一部分内容：学习目标 结合具体函数，了解函数奇偶性的含义，掌握判断函数奇偶性的方法 了解函数奇偶性与函数图像对称性之间的关系 会利用函数的奇偶性解决简单问题 ... ... ... 函数的奇偶性PPT，第二部分内容：自主学习 问题导学 预习教材P104－P109的内容，思考以下问题： 1．奇函数与偶函数的定义是什么？ 2．奇、偶函数的定义域有什么特点？ 3．奇、偶函数的图像有什么特征？ 新知初探 1．偶函数 (1)定义：一般地，设函数y＝f(x)的定义域为D，如果对D内的任意一个x，都有____________，且____________，则称y＝f(x)为偶函数． (2)图像特征：图像关于______对称． 2．奇函数 (1)定义：一般地，设函数y＝f(x)的定义域为D，如果对D内的任意一个x，都有____________，且__________________，则称y＝f(x)为奇函数． (2)图像特征：图像关于______对称． ■名师点拨 (1)奇、偶函数定义域的特点 由于f(x)和f(－x)须同时有意义，所以奇、偶函数的定义域关于原点对称． (2)奇、偶函数的对应关系的特点 ①奇函数有f(－x)＝－f(x)⇔f(－x)＋f(x)＝0⇔f(－x)f(x)＝－1(f(x)≠0)； ②偶函数有f(－x)＝f(x)⇔f(－x)－f(x)＝0⇔f(－x)f(x)＝1(f(x)≠0)． (3)函数奇偶性的三个关注点 ①若奇函数在原点处有定义，则必有f(0)＝0.有时可以用这个结论来否定一个函数为奇函数； ②既是奇函数又是偶函数的函数只有一种类型，即f(x)＝0，x∈I，其中定义域I是关于原点对称的非空集合； ③函数根据奇偶性可分为奇函数、偶函数、既奇又偶函数、非奇非偶函数． 自我检测 判断正误(正确的打“√”，错误的打“×”) (1)奇、偶函数的定义域都关于原点对称．(　　) (2)函数f(x)＝x2的图像关于原点对称．(　　) (3)对于定义在R上的函数f(x)，若f(－1)＝－f(1)，则函数f(x)一定是奇函数．(　　) (4)若f(x)是定义在R上的奇函数，则f(－x)＋f(x)＝0.(　　) 下列函数为奇函数的是(　　) A．y＝|x|　B．y＝3－x C．y＝1x3  D．y＝－x2＋14 若函数y＝f(x)，x∈[－2，a]是偶函数，则a的值为(　　) A．－2  B．2 C．0  D．不能确定 ... ... ... 函数的奇偶性PPT，第三部分内容：讲练互动 函数奇偶性的判断 判断下列函数的奇偶性： (1)f(x)＝|x＋1|－|x－1|； (2)f(x)＝x2－1＋ 1－x2； (3)f(x)＝1－x2x； (4)f(x)＝x＋1，x>0，－x＋1，x<0. 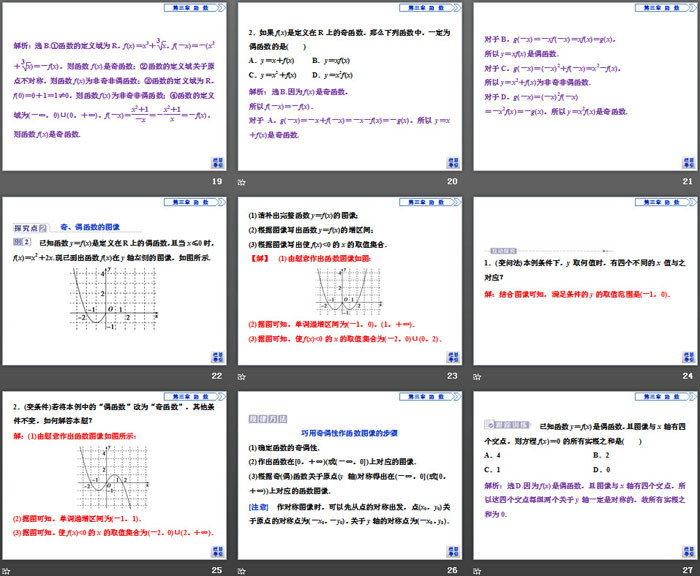规律方法 判断函数奇偶性的两种方法 (1)定义法 (2)图像法 [注意]对于分段函数奇偶性的判断，应分段讨论，要注意根据x的范围取相应的函数解析式．　  奇、偶函数的图像 已知函数y＝f(x)是定义在R上的偶函数，且当x≤0时，f(x)＝x2＋2x.现已画出函数f(x)在y轴左侧的图像，如图所示． (1)请补出完整函数y＝f(x)的图像； (2)根据图像写出函数y＝f(x)的增区间； (3)根据图像写出使f(x)<0的x的取值集合． 规律方法 巧用奇偶性作函数图像的步骤 (1)确定函数的奇偶性． (2)作出函数在[0，＋∞)(或(－∞，0])上对应的图像． (3)根据奇(偶)函数关于原点(y轴)对称得出在(－∞，0](或[0，＋∞))上对应的函数图像． [注意]作对称图像时，可以先从点的对称出发，点(x0，y0)关于原点的对称点为(－x0，－y0)，关于y轴的对称点为(－x0，y0)． ... ... ... 函数的奇偶性PPT，第四部分内容：达标反馈 1．下列函数是偶函数的是(　　) A．y＝x B．y＝2x2－3 C．y＝x D．y＝x2，x∈(－1，1] 2．函数f(x)＝1x－x的图像关于(　　) A．y轴对称 B．直线y＝－x对称 C．坐标原点对称 D．直线y＝x对称 3．已知函数f(x)为R上的奇函数，且当x＞0时，f(x)＝x2＋1x，则f(－1)＝________． 4．根据题中函数的奇偶性及所给部分图像，作出函数在y轴另一侧的图像，并解决问题： (1)如图①是奇函数y＝f(x)的部分图像，求f(－4)•f(－2)； (2)如图②是偶函数y＝f(x)的部分图像，比较f(1)与f(3)的大小． ... ... ... 关键词：高中人教B版数学必修一PPT课件免费下载，函数的奇偶性PPT下载，函数的概念与性质PPT下载，函数奇偶性的概念PPT下载，.PPT格式；