《函数的奇偶性》函数的概念与性质PPT(第1课时奇偶性的概念)

《函数的奇偶性》函数的概念与性质PPT(第1课时奇偶性的概念) 第一部分内容：学 习 目 标 1.理解奇函数、偶函数的定义． 2．了解奇函数、偶函数图像的特征． 3．掌握判断函数奇偶性的方法. 核 心 素 养 1.借助奇(偶)函数的特征，培养直观想象素养． 2．借助函数奇、偶的判断方法，培养逻辑推理素养. ... ... ... 函数的奇偶性PPT，第二部分内容：自主预习探新知 新知初探 条件  设函数y＝f(x)的定义域为D，如果对D内的任意一个x，都有－x∈D 结论 f(－x)＝f(x)      f(－x)＝－f(x) 图像特点 关于____对称   关于____对称 思考：具有奇偶性的函数，其定义域有何特点？ 提示：定义域关于原点对称． 初试身手 1．下列函数是偶函数的是(　　) A．y＝x　B．y＝2x2－3 C．y＝1x  D．y＝x2，x∈[0,1] 2．下列图像表示的函数具有奇偶性的是(　　) B　[B选项的图像关于y轴对称，是偶函数，其余选项中的图像都不具有奇偶性．] 3．函数y＝f(x)，x∈[－1，a](a>－1)是奇函数，则a等于(　　) A．－1　B．0  C．1　D．无法确定 4．若f(x)为R上的偶函数，且f(2)＝3，则f(－2)＝________. ... ... ... 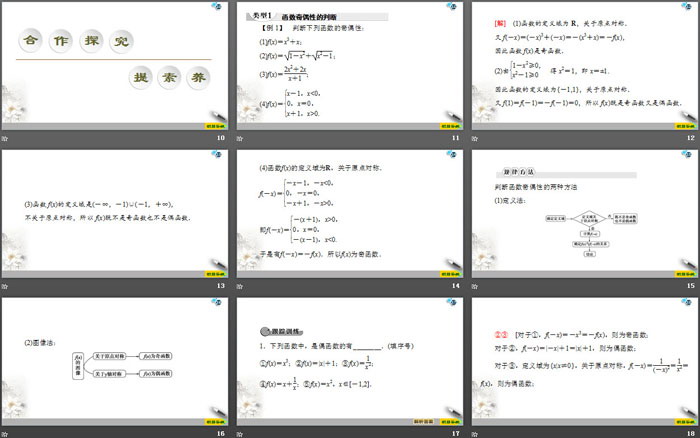函数的奇偶性PPT，第三部分内容：合作探究提素养 函数奇偶性的判断 【例1】判断下列函数的奇偶性： (1)f(x)＝x3＋x； (2)f(x)＝1－x2＋x2－1； (3)f(x)＝2x2＋2xx＋1； (4)f(x)＝x－1，x<0，0，x＝0，x＋1，x>0. [解]　(1)函数的定义域为R，关于原点对称． 又f(－x)＝(－x)3＋(－x)＝－(x3＋x)＝－f(x)， 因此函数f(x)是奇函数． (2)由1－x2≥0，x2－1≥0得x2＝1，即x＝±1. 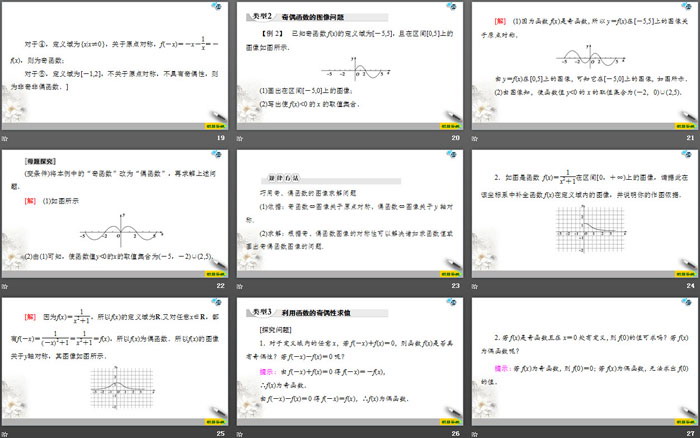因此函数的定义域为{－1,1}，关于原点对称． 又f(1)＝f(－1)＝－f(－1)＝0，所以f(x)既是奇函数又是偶函数． (3)函数f(x)的定义域是(－∞，－1)∪(－1，＋∞)， 不关于原点对称，所以f(x)既不是奇函数也不是偶函数． 奇偶函数的图像问题 【例2】已知奇函数f(x)的定义域为[－5,5]，且在区间[0,5]上的图像如图所示． (1)画出在区间[－5,0]上的图像； (2)写出使f(x)<0的x的取值集合． [解](1)因为函数f(x)是奇函数，所以y＝f(x)在[－5,5]上的图像关于原点对称． 由y＝f(x)在[0,5]上的图像，可知它在[－5,0]上的图像，如图所示． (2)由图像知，使函数值y<0的x的取值集合为(－2，0)∪(2,5)． 规律方法 巧用奇、偶函数的图像求解问题 1依据：奇函数⇔图像关于原点对称，偶函数⇔图像关于y轴对称. 2求解：根据奇、偶函数图像的对称性可以解决诸如求函数值或画出奇偶函数图像的问题. 2．如图是函数f(x)＝1x2＋1在区间[0，＋∞)上的图像，请据此在该坐标系中补全函数f(x)在定义域内的图像，并说明你的作图依据． 利用函数的奇偶性求值 [探究问题] 1．对于定义域内的任意x，若f(－x)＋f(x)＝0，则函数f(x)是否具有奇偶性？若f(－x)－f(x)＝0呢？ 提示：由f(－x)＋f(x)＝0得f(－x)＝－f(x)， ∴f(x)为奇函数． 由f(－x)－f(x)＝0得f(－x)＝f(x)，∴f(x)为偶函数． 2．若f(x)是奇函数且在x＝0处有定义，则f(0)的值可求吗？若f(x)为偶函数呢？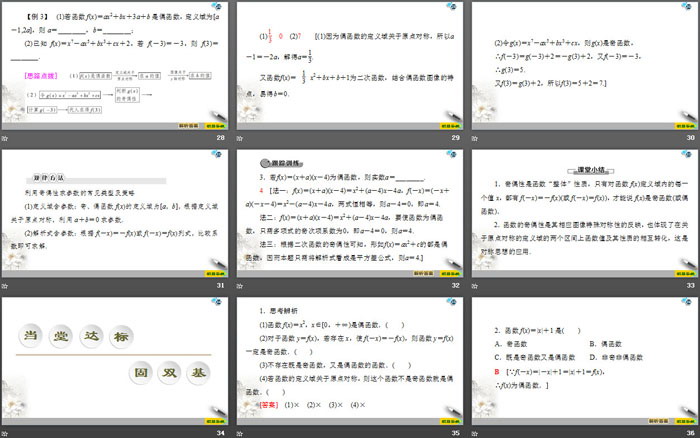 提示：若f(x)为奇函数，则f(0)＝0；若f(x)为偶函数，无法求出f(0)的值． 规律方法 利用奇偶性求参数的常见类型及策略 1定义域含参数：奇、偶函数fx的定义域为[a，b]，根据定义域关于原点对称，利用a＋b＝0求参数. 2解析式含参数：根据f(－x)＝－f(x)或f(－x)＝f(x)列式，比较系数即可求解. 课堂小结 1．奇偶性是函数“整体”性质，只有对函数f(x)定义域内的每一个值x，都有f(－x)＝－f(x)(或f(－x)＝f(x))，才能说f(x)是奇函数(或偶函数)． 2．函数的奇偶性是其相应图像特殊对称性的反映，也体现了在关于原点对称的定义域的两个区间上函数值及其性质的相互转化，这是对称思想的应用. ... ... ... 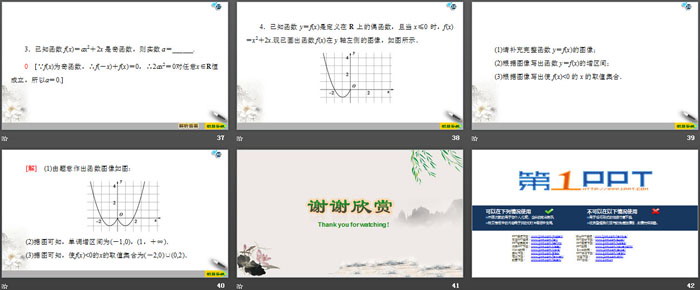函数的奇偶性PPT，第四部分内容：当堂达标固双基 1．思考辨析 (1)函数f(x)＝x2，x∈[0，＋∞)是偶函数．(　　) (2)对于函数y＝f(x)，若存在x，使f(－x)＝－f(x)，则函数y＝f(x)一定是奇函数．(　　) (3)不存在既是奇函数，又是偶函数的函数．(　　) (4)若函数的定义域关于原点对称，则这个函数不是奇函数就是偶函数．(　　) 2．函数f(x)＝|x|＋1是(　　) A．奇函数　B．偶函数 C．既是奇函数又是偶函数  D．非奇非偶函数 3．已知函数f(x)＝ax2＋2x是奇函数，则实数a＝______. 4．已知函数y＝f(x)是定义在R上的偶函数，且当x≤0时，f(x)＝x2＋2x.现已画出函数f(x)在y轴左侧的图像，如图所示． (1)请补充完整函数y＝f(x)的图像； (2)根据图像写出函数y＝f(x)的增区间； (3)根据图像写出使f(x)<0的x的取值集合． ... ... ... 关键词：高中人教B版数学必修一PPT课件免费下载，函数的奇偶性PPT下载，函数的概念与性质PPT下载，奇偶性的概念PPT下载，.PPT格式；