人教A版(2019)数学必修第一册《三角函数的概念》三角函数PPT(第1课时三角函数的概念)
展开
《三角函数的概念》三角函数PPT(第1课时三角函数的概念)
第一部分内容:学习目标
理解三角函数的概念,会求给定角的三角函数值
掌握各象限角的三角函数值的符号规律
掌握三角函数诱导公式一的简单应用
... ... ...
三角函数的概念PPT,第二部分内容:自主学习
问题导学
预习教材P177-P181,并思考以下问题:
1.任意角的三角函数的定义是什么?
2.如何判断三角函数值在各象限内的符号?
3.诱导公式一是什么?
新知初探
1.任意角的三角函数的定义
■名师点拨
(1)在任意角的三角函数的定义中,应该明确:α是一个任意角,其范围是使函数有意义的实数集.
(2)要明确sin α是一个整体,不是sin与α的乘积,它是“正弦函数”的一个记号,就如f(x)表示自变量为x的函数一样,离开自变量的“sin”“cos”“tan”等是没有意义的.
2.三角函数值的符号
如图所示:
正弦:______象限正,______象限负;
余弦:______象限正,______象限负;
正切:______象限正,______象限负.
简记口诀:一全正、二正弦、三正切、四余弦.
3.公式一
终边相同的角的同一三角函数的值______,由此得到一组公式(公式一):
sin(α+k•2π)=____________,
cos(α+k•2π)=____________,
tan(α+k•2π)=____________,
其中k∈Z.
■名师点拨
(1)公式一的实质
公式一的实质是终边相同的角,其同名三角函数值相等.因为这些角的终边是同一条射线,所以根据三角函数的定义可知,这些角的三角函数值相等.
(2)公式一的作用
利用公式一可以把任意角的三角函数值化为0°~360°范围内与其终边相同的角的三角函数值(方法是先在0°~360°的范围内找出与所给角终边相同的角,再把它写成公式一的形式,最后得出结果).
自我检测
判断正误(正确的打“√”,错误的打“×”)
(1)已知α是三角形的内角,则必有sin α>0,cos α≥0.( )
(2)若sin α•cos α>0,则角α为第一象限角.( )
(3)对于任意角α,三角函数sin α、cos α、tan α都有意义.( )
(4)三角函数值的大小与点P(x,y)在终边上的位置无关. ( )
(5)同一个三角函数值能找到无数个角与之对应.( )
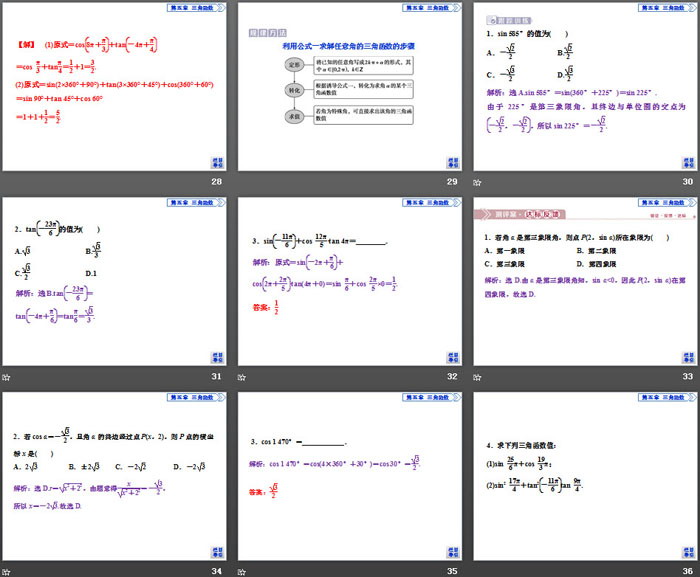
已知sin α=35,cos α=-45,则角α所在的象限是( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
已知角α的终边经过P(-b,4),且cos α=-35,则b的值为( )
A.3 B.-3
C.±3 D.5
... ... ...
三角函数的概念PPT,第三部分内容:讲练互动
求任意角的三角函数值
(1)已知角α的终边与单位圆的交点为P35,y(y<0),求tan α的值.
(2)已知角α的终边落在射线y=2x(x≥0)上,求sin α,cos α的值.
互动探究
1.(变条件)本例(2)中条件“角α的终边落在射线y=2x(x≥0)上”变为“角α的终边为射线y=-34x(x≥0)”,求角α的正弦、余弦和正切值.
2.(变条件)本例(2)中条件“α的终边落在射线y=2x(x≥0)上”变为“α的终边落在直线y=2x上”,其他条件不变,其结论又如何呢?
规律方法
已知α终边上任意一点的坐标求三角函数值的方法
(1)先利用直线与单位圆相交,求出交点坐标,然后再利用正、余弦函数的定义求出相应三角函数值.
(2)在α的终边上任选一点P(x,y),P到原点的距离为r(r>0),则sin α=yr,cos α=xr.已知α的终边求α的三角函数值时,用这几个公式更方便.
(3)当角α的终边上点的坐标以参数形式给出时,要根据问题的实际情况对参数进行分类讨论.
三角函数值符号的判定
判断下列各式的符号:
(1)tan 120°sin 269°;
(2)cos 4tan-23π4.
【解】(1)因为120°角是第二象限角,
所以tan 120°<0.
因为269°角是第三象限角,
所以sin 269°<0.
所以tan 120°sin 269°>0.
跟踪训练
1.若-π2<α<0,则点(tan α,cos α)位于( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
2.(2019•安徽太和中学第一次教学质量检测)已知sin θcos θ<0,且|cos θ|=cos θ,则角θ是( )
A.第一象限角 B.第二象限角
C.第三象限角 D.第四象限角
... ... ...
三角函数的概念PPT,第四部分内容:达标反馈
1.若角α是第三象限角,则点P(2,sin α)所在象限为( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
2.若cos α=-32,且角α的终边经过点P(x,2),则P点的横坐标x是( )
A.23 B.±23 C.-22 D.-23
3.cos 1 470°=____________.
... ... ...
关键词:高中人教A版数学必修一PPT课件免费下载,三角函数的概念PPT下载,三角函数PPT下载,.PPT格式;