人教A版(2019)数学必修第一册《三角函数的图象与性质》三角函数PPT(第四课时正切函数的性质与图象)
展开
《三角函数的图象与性质》三角函数PPT(第四课时正切函数的性质与图象)
第一部分内容:学习目标
掌握正切函数的定义域、值域
会利用正切函数图象研究其单调性,并利用单调性解决其相应问题
掌握正切函数的周期性及奇偶性
... ... ...
三角函数的图象与性质PPT,第二部分内容:自主学习
问题导学
预习教材P209-P212,并思考以下问题:
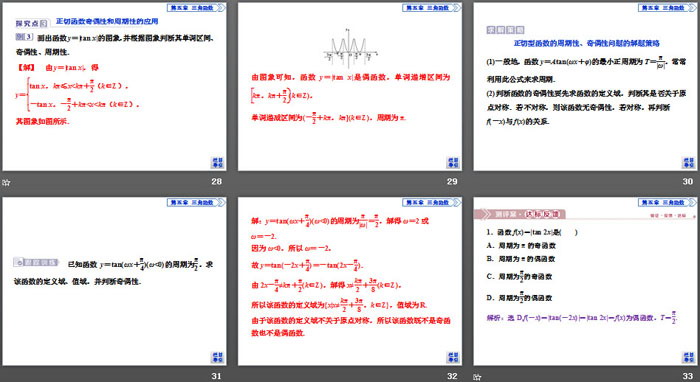
1.如何借助单位圆画正切函数图象?
2.正切函数的性质与正弦函数性质有何不同?
3.正切函数在定义域内是不是单调函数?
新知初探
函数y=tan x的图象与性质
■名师点拨
(1)正切函数在每一个开区间-π2+kπ,π2+kπ(k∈Z)内是增函数.不能说函数在其定义域内是单调递增函数,无单调递减区间.
(2)画正切函数图象常用三点两线法:“三点”是指(-π4,-1),(0,0),(π4,1),“两线”是指x=-π2和x=π2,大致画出正切函数在(-π2,π2)上的简图后向左、向右扩展即得正切曲线.
自我检测
判断正误(正确的打“√”,错误的打“×”)
(1)正切函数的定义域和值域都是R.( )
(2)正切函数在整个定义域上是增函数.( )
(3)正切函数在定义域内无最大值和最小值.( )
(4)存在某个区间,使正切函数为减函数.( )
函数f(x)=tanx+π6的定义域是( )
A.x|x∈R,x≠kπ-π2,k∈Z
B.{x|x∈R,x≠kπ,k∈Z}
C.x|x∈R,x≠kπ+π6,k∈Z
D.x|x∈R,x≠kπ+π3,k∈Z
函数y=tan2x+π4的最小正周期为( )
A.π2 B.π
C.2π D.3π
函数f(x)=tan x在[-π3,π4]上的最小值为________.
函数y=tanx-π4的单调递增区间是________.
... ... ...
三角函数的图象与性质PPT,第三部分内容:讲练互动
正切函数的定义域、值域
(1)函数 y=tan(2x-π4)的定义域是________.
(2)函数y=tan2x+4tan x-1的值域是________.
规律方法
求正切函数定义域的方法
(1)①求与正切函数有关的函数的定义域时,除了求函数定义域的一般要求外,还要保证正切函数y=tan x有意义,即x≠π2+kπ,k∈Z.
②求正切型函数y=Atan(ωx+φ)(A≠0,ω>0)的定义域时,要将“ωx+φ”视为一个“整体”.令ωx+φ≠kπ+π2,k∈Z,解得x.
(2)求正切函数值域的方法
①对于y=Atan(ωx+φ)的值域,可以把ωx+φ看成整体,结合图象,利用单调性求值域.
②对于与y=tan x相关的二次函数,可以把tan x看成整体,利用配方法求值域.
正切函数的单调性及其应用
(1)求y=tan12x+π4的单调区间.
(2)比较tan 65π与tan-137π的大小.
规律方法
(1)运用正切函数单调性比较大小的方法
①运用函数的周期性或诱导公式将角化到同一单调区间内.
②运用单调性比较大小关系.
(2)求函数y=Atan(ωx+φ)(A,ω,φ都是常数)的单调区间的方法
①若ω>0,由于y=tan x在每一个单调区间上都是增函数,故可用“整体代换”的思想,令kπ-π2<ωx+φ<kπ+π2,k∈Z,解得x的范围即可.
②若ω<0,可利用诱导公式先把y=Atan(ωx+φ)转化为y=Atan[-(-ωx-φ)]=-Atan(-ωx-φ),即把x的系数化为正值,再利用“整体代换”的思想,求得x的范围即可.
... ... ...
三角函数的图象与性质PPT,第四部分内容:达标反馈
1.函数f(x)=|tan 2x|是( )
A.周期为π的奇函数
B.周期为π的偶函数
C.周期为π2的奇函数
D.周期为π2的偶函数
2.比较大小:tan 13π4________tan17π5.
3.求函数y=tan(3x-π3)的定义域、周期,并指出它的单调区间.
关键词:高中人教A版数学必修一PPT课件免费下载,三角函数的图象与性质PPT下载,三角函数PPT下载,正切函数的性质与图象PPT下载,.PPT格式;