人教版(2012)数学九年级下册《相似三角形应用举例》相似PPT(第2课时)
展开
《相似三角形应用举例》相似PPT(第2课时)
例题解析
例 如图,左、右并排的两棵大树的高分别是AB=8 m和CD=12 m,两树底部的距离BD=5 m.一个人估计自己眼睛距地面1.6 m.她沿着正对这两棵树的一条水平直路l从左向右前进,当他与左边较低的树的距离小于多少时,就看不到右边较高的树的顶端C了?
分析:如图,设观察者眼睛的位置为点F,画出观察者的水平视线FG,分别交AB,CD于点H,K. 视线FA与FG的夹角∠AFH是观察点A时的仰角 . 类似地,∠CFK是观察点C时的仰角.由于树的遮挡,区域Ⅰ和Ⅱ ,观测者都看不到.
例 我国魏晋时期数学家刘徽的《海岛算经》中有一题:今有望海岛,立两表齐高三丈,前后相去千步,今后表与前表参相直,从前表却行一百二十三步,人目着地取望岛峰亦与表末参合,从后表却行一百二十七步,人目看地取望岛峰亦与表末参合,问岛高及去表各几何?画成图形,用现在的话表述即是:要求海岛的山峰AB的高度,分别在D和F处树立标杆DC和FE,标杆高都是3丈,相隔1 000步(一步等于5尺),并且AB,CD,EF都在同一截面上.从标杆DC退后123步的G处,可看见山峰顶A和标杆顶C在同一直线上;
从标杆FE退后127步的H处,也可以看到山峰顶A和标杆顶E在同一直线上,求山高AB及它和标杆CD的水平距离BD.
例 如图所示,一段街道的两边缘所在直线分别为AB,PQ,并且AB∥
PQ.建筑物的一端DE所在直线MN⊥AB于点M,交PQ于点N.小亮从胜利街的点A处,沿着AB方向前进,小明一直站在点P的位置等候小亮.
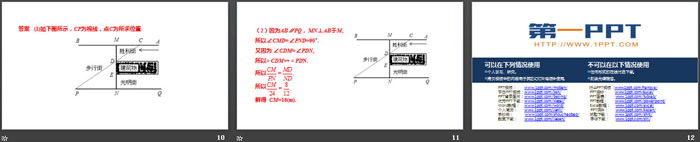
(1)请你在图中画出小亮恰好能看见小明时的视线,以及此时小亮所在位置(用点C标出);
(2)已知MN=20 m, MD=8 m , PN=24 m,
求(1)中的点C到胜利街口的距离CM.
关键词:人教版九年级下册数学PPT课件免费下载,相似三角形应用举例PPT下载,相似PPT下载,.PPT格式;