人教版(2019)化学必修第一册《章末复习课》三角函数PPT
展开
《章末复习课》三角函数PPT
同角三角函数基本关系和诱导公式的应用
【例1】(1)已知sin(-π+θ)+2cos(3π-θ)=0,则sin θ+cos θsin θ-cos θ=________.
(2)已知f(α)=sin2π-α•cos2π-α•tan-π+αsin-π+α•tan-α+3π.
①化简f(α);
②若f(α)=18,且π4<α<π2,求cos α-sin α的值;
③若α=-47π4,求f(α)的值.
[思路点拨]先用诱导公式化简,再用同角三角函数基本关系求值.
母题探究
1.将本例(2)中“18”改为“-18”“π4<α<π2”改为“-π4<α<0”求cos α+sin α.
[解] 因为-π4<α<0,所以cos α>0,sin α<0且|cos α|>|sin α|,
所以cos α+sin α>0,
又(cos α+sin α)2=1+2sin αcos α=1+2×-18=34,所以cos α+sin α=32.
2.将本例(2)中的用tan α表示1fα+cos2α.
[解] 1fα+cos2α=1sin αcos α+cos2α
=sin2α+cos2αsin αcos α+cos2α=tan2α+1tan α+1.
规律方法
1.牢记两个基本关系式sin2α+cos2α=1及sin αcos α=tan α,并能应用两个关系式进行三角函数的求值、化简、证明.在应用中,要注意掌握解题的技巧.比如:已知sin α±cos α的值,可求cos αsin α.注意应用(cos α±sin α)2=1±2sin αcos α.
2.诱导公式可概括为k•π2±α(k∈Z)的各三角函数值的化简公式.记忆规律是:奇变偶不变,符号看象限.
三角函数的图象变换问题
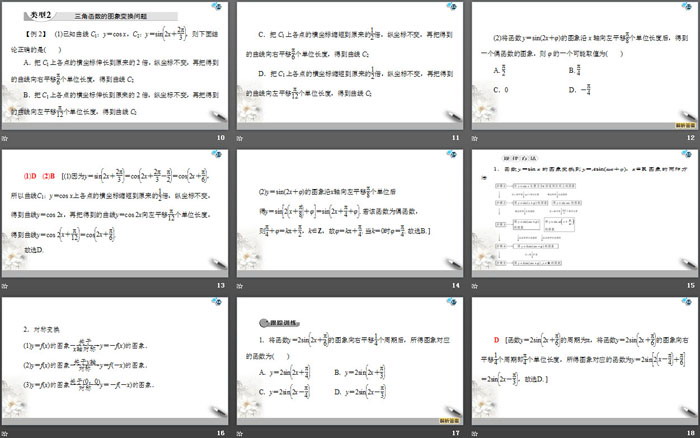
【例2】(1)已知曲线C1:y=cos x,C2:y=sin2x+2π3,则下面结论正确的是( )
A.把C1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移π6个单位长度,得到曲线C2
B.把C1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向左平移π12个单位长度,得到曲线C2
C.把C1上各点的横坐标缩短到原来的12倍,纵坐标不变,再把得到的曲线向右平移π6个单位长度,得到曲线C2
D.把C1上各点的横坐标缩短到原来的12倍,纵坐标不变,再把得到的曲线向左平移π12个单位长度,得到曲线C2
(2)将函数y=sin(2x+φ)的图象沿x轴向左平移π8个单位长度后,得到一个偶函数的图象,则φ的一个可能取值为( )
A.π2 B.π4
C.0 D.-π4
规律方法
1.函数y=sin x的图象变换到y=Asin(ωx+φ),x∈R图象的两种方法
2.对称变换
(1)y=f(x)的图象�D�D�D�D→关于x轴对称y=-f(x)的图象.
(2)y=f(x)的图象�D�D�D�D→关于y轴对称y=f(-x)的图象.
(3)y=f(x)的图象�D�D�D�D→关于0,0对称y=-f(-x)的图象.
三角函数的性质
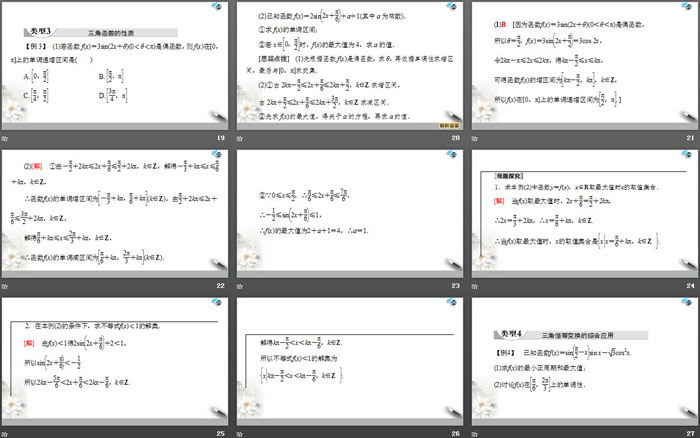
【例3】(1)若函数f(x)=3sin(2x+θ)(0<θ<π)是偶函数,则f(x)在[0,π]上的单调递增区间是( )
A.0,π2 B.π2,π
C.π4,π2 D.3π4,π
(2)已知函数f(x)=2sin2x+π6+a+1(其中a为常数).
①求f(x)的单调区间;
②若x∈0,π2时,f(x)的最大值为4,求a的值.
[思路点拨] (1)先根据函数f(x)是偶函数,求θ,再依据单调性求增区间,最后与[0,π]求交集.
(2)①由2kπ-π2≤2x+π6≤2kπ+π2,k∈Z求增区间,
由2kπ+π2≤2x+π6≤2kπ+3π2,k∈Z求减区间.
②先求f(x)的最大值,得关于a的方程,再求a的值.
... ... ...
关键词:高中人教A版数学必修一PPT课件免费下载,章末复习课PPT下载,三角函数PPT下载,.PPT格式;