《函数及其表示方法》函数的概念与性质PPT(第1课时函数的概念)

《函数及其表示方法》函数的概念与性质PPT(第1课时函数的概念) 第一部分内容：学习目标 理解函数的概念，了解构成函数的三要素 会求一些简单函数的定义域 掌握同一个函数的概念，并会判断 会求简单函数的函数值和值域 ... ... ... 函数及其表示方法PPT，第二部分内容：自主学习 问题导学 预习教材P85－P88的内容，思考以下问题： 1．函数的概念是什么？ 2．函数的自变量、定义域是如何定义的？ 3．函数的值域是如何定义的？ 新知初探 1．函数的有关概念 一般地，给定两个非空实数集A与B，以及对应关系f，如果对于集合A中的每一个实数x，按照对应关系f，在集合B中都有___________的实数y＝f(x)与x对应，则称f为定义在集合A上的一个函数，记作____________________，其中x称为__________，y称为__________，自变量取值的范围(即数集A)称为这个函数的__________，所有函数值组成的集合_____________________，称为函数的值域． ■名师点拨 对函数概念的5点说明 (1)当A，B为非空数集时，符号“f：A→B”表示A到B的一个函数． (2)集合A中的数具有任意性，集合B中的数具有唯一性． (3)符号“f”表示对应关系，在不同的函数中f的具体含义不一样． (4)函数的定义强调的是“对应关系”，对应关系也可用小写英文字母如g，h表示． (5)在函数的表示中，自变量与因变量与用什么字母表示无关紧要，如f(x)＝2x＋1，x∈R与y＝2s＋1，s∈R是同一个函数． 2．同一个函数 如果两个函数表达式表示的函数________相同，___________也相同(即对自变量的每一个值，两个函数表达式得到的函数值都相等)，则称这两个函数表达式表示的就是同一个函数． 自我检测 判断正误(正确的打“√”，错误的打“×”) (1)任何两个集合之间都可以建立函数关系．(　　) (2)已知定义域和对应关系就可以确定一个函数．(　　) (3)根据函数的定义，定义域中的每一个x可以对应着不同的y.(　　) 已知函数g(x)＝2x2－1，则g(1)＝(　　) A．－1　B．0 C．1     D．2 函数f(x)＝14－x的定义域是(　　) A．(－∞，4)  B．(－∞，4] C．(4，＋∞)  D．[4，＋∞) 下列式子中不能表示函数y＝f(x)的是(　　) A．x＝y2＋1  B．y＝2x2＋1 C．x－2y＝6  D．x＝y ... ... ... 函数及其表示方法PPT，第三部分内容：讲练互动 函数的概念 (1)如图可作为函数y＝f(x)的图像的是(　　) (2)下列三个说法： ①若函数的值域只含有一个元素，则定义域也只含有一个元素； ②若f(x)＝5(x∈R)，则f(π)＝5一定成立； ③函数就是两个集合之间的对应关系． 其中正确说法的个数为(　　) A．0　 　 B．1　 　 C．2　 　 D．3 (3)已知集合A＝[0，8]，集合B＝[0，4]，则下列对应关系中，不能看作是从A到B的函数关系的是(　　) A．f：x→y＝18x  B．f：x→y＝14x C．f：x→y＝12x  D．f：x→y＝x 规律方法 (1)判断所给对应关系是否为函数的方法 ①先观察两个数集A，B是否非空； ②验证对应关系下，集合A中x的任意性，集合B中y的唯一性． (2)根据图形判断对应关系是否为函数的步骤 ①任取一条垂直于x轴的直线l； ②在定义域内平行移动直线l； ③若l与图形有且只有一个交点，则是函数；若在定义域内没有交点或有两个或两个以上的交点，则不是函数． 求函数的定义域 求下列函数的定义域： (1)y＝(x＋1)2x＋1－1－x；(2)y＝3－x|x|－5. 规律方法  (1)求函数定义域的常用方法 ①若f(x)是分式，则应考虑使分母不为零； ②若f(x)是偶次根式，则被开方数大于或等于零； ③若f(x)是指数幂，则函数的定义域是使幂运算有意义的实数集合； ④若f(x)是由几个式子构成的，则函数的定义域是几个部分定义域的交集； ⑤若f(x)是实际问题的解析式，则应符合实际问题，使实际问题有意义． (2)第(1)题易出现化简y＝x＋1－1－x，错求定义域为{x|x≤1}，在求函数定义域时，不能盲目对函数式变形．　  同一个函数 (1)给出下列三个说法： ①f(x)＝x0与g(x)＝1是同一个函数；②y＝f(x)，x∈R与y＝f(x＋1)，x∈R可能是同一个函数；③y＝f(x)，x∈R与y＝f(t)，t∈R是同一个函数． 其中正确说法的个数是(　　) A．3  B．2 C．1  D．0 (2)下列各组函数： ①f(x)＝x2－xx，g(x)＝x－1； ②f(x)＝xx，g(x)＝xx； ③f(x)＝x＋1•1－x，g(x)＝1－x2； ④f(x)＝(x＋3)2，g(x)＝x＋3. 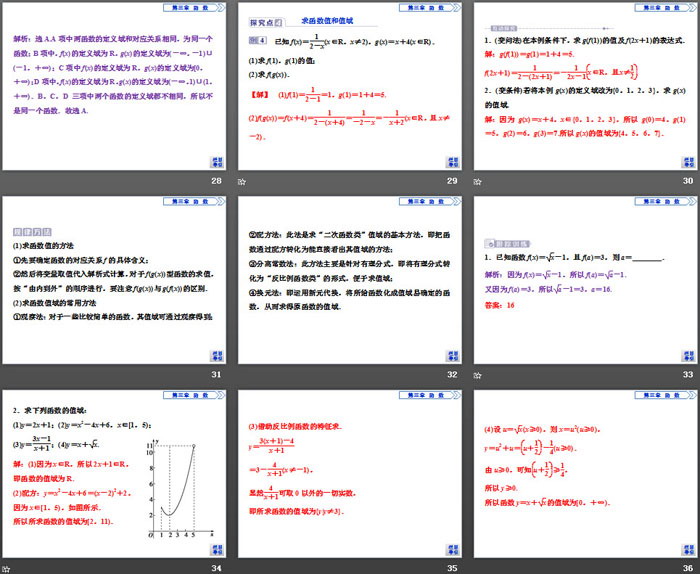其中表示同一个函数的是________(填上所有同一个函数的序号)． 反思归纳 判断两个函数为同一个函数应注意的三点 (1)定义域、对应关系两者中只要有一个不相同就不是同一个函数，即使定义域与值域都相同，也不一定是同一个函数． (2)函数是两个非空数集之间的对应关系，所以用什么字母表示自变量、因变量是没有限制的． (3)在化简解析式时，必须是等价变形．　  求函数值和值域 已知f(x)＝12－x(x∈R，x≠2)，g(x)＝x＋4(x∈R)． (1)求f(1)，g(1)的值； (2)求f(g(x))． 互动探究 1．(变问法)在本例条件下，求g(f(1))的值及f(2x＋1)的表达式． 2．(变条件)若将本例g(x)的定义域改为{0，1，2，3}，求g(x)的值域． 规律方法 (1)求函数值的方法 ①先要确定函数的对应关系f的具体含义； ②然后将变量取值代入解析式计算，对于f(g(x))型函数的求值，按“由内到外”的顺序进行，要注意f(g(x))与g(f(x))的区别． (2)求函数值域的常用方法 ①观察法：对于一些比较简单的函数，其值域可通过观察得到； ②配方法：此法是求“二次函数类”值域的基本方法，即把函数通过配方转化为能直接看出其值域的方法； ③分离常数法：此方法主要是针对有理分式，即将有理分式转化为“反比例函数类”的形式，便于求值域； ④换元法：即运用新元代换，将所给函数化成值域易确定的函数，从而求得原函数的值域．　  ... ... ... 函数及其表示方法PPT，第四部分内容：达标反馈 1．若f(x)＝x＋1，则f(3)＝(　　) A．2　　　B．4 C．22  D．10 2．对于函数f：A→B，若a∈A，则下列说法错误的是(　　) A．f(a)∈B B．f(a)有且只有一个 C．若f(a)＝f(b)，则a＝b D．若a＝b，则f(a)＝f(b) 3．已知函数f(x)＝2x－3，x∈{x∈N|1≤x≤5}，则函数f(x)的值域为________． 4．已知函数f(x)＝6x－1－x＋4. (1)求函数f(x)的定义域； (2)求f(－1)，f(12)的值． ... ... ... 关键词：高中人教B版数学必修一PPT课件免费下载，函数及其表示方法PPT下载，函数的概念与性质PPT下载，函数的概念PPT下载，.PPT格式；