人教A版(2019)数学必修第二册《章末复习提升课》函数PPT
展开
《章末复习提升课》函数PPT
第一部分内容:综合提高
函数的定义域和值域
(1)函数f(x)=3x21-x+(3x-1)0的定义域是( )
A.-∞,13 B.13,1
C.-13,13 D.-∞,13∪13,1
(2)已知函数y=f(x+1)的定义域是[-2,3],则y=f(2x-1)的定义域是( )
A.0,52 B.[-1,4]
C.[-5,5] D.[-3,7]
(3)求下列函数的值域:
①y=2x+1x-3;
②y=x+41-x;
③y=1x-2x,x∈-2,-12.
规律方法
求函数定义域的类型与方法
(1)已给出函数解析式:函数的定义域是使解析式有意义的自变量的取值集合.
(2)实际问题:求函数的定义域既要考虑解析式有意义,还应考虑使实际问题有意义.
(3)复合函数问题:
①若f(x)的定义域为[a,b],f(g(x))的定义域应由a≤g(x)≤b解出;
②若f(g(x))的定义域为[a,b],则f(x)的定义域为g(x)在[a,b]上的值域.
[注意](1)f(x)中的x与f(g(x))中的g(x)地位相同.
(2)定义域所指永远是自变量的范围.
跟踪训练
1.设函数f(x)的定义域为[1,5],则函数f(2x-3)的定义域为( )
A.[2,4] B.[3,11]
C.[3,7] D.[1,5]
2.设函数f(x)=-2x2+4x在区间[m,n]上的值域是[-6,2],则m+n的取值范围是_________.
函数的解析式
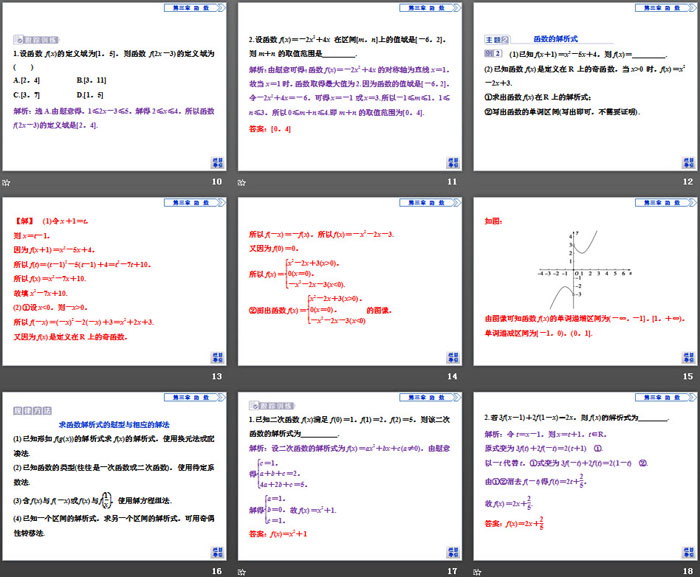
(1)已知f(x+1)=x2-5x+4,则f(x)=_________.
(2)已知函数f(x)是定义在R上的奇函数,当x>0时,f(x)=x2-2x+3.
①求出函数f(x)在R上的解析式;
②写出函数的单调区间(写出即可,不需要证明).
规律方法
求函数解析式的题型与相应的解法
(1)已知形如f(g(x))的解析式求f(x)的解析式,使用换元法或配凑法.
(2)已知函数的类型(往往是一次函数或二次函数),使用待定系数法.
(3)含f(x)与f(-x)或f(x)与f1x,使用解方程组法.
(4)已知一个区间的解析式,求另一个区间的解析式,可用奇偶性转移法.
... ... ...
章末复习提升课PPT,第二部分内容:素养提升
1.函数f(x)=2x2,x∈[0,1],2,x∈(1,2),x+1,x∈[2,+∞)的值域是( )
A.R B.(0,2)∪(2,+∞)
C.(0,+∞) D.[0,2]∪[3,+∞)
2.(2019•沈阳期末)已知函数y=kx-2(k≠0)在[3,8]上的最大值为1,则k的值为( )
A.1 B.-6
C.1或-6 D.6
3.若f(x)=3ax-2a+1,若存在x0∈(-1,1),使f(x0)=0成立,则实数a的取值范围是( )
A.-1<a<15 B.a<1
C.a<-1或a>15 D.a>15
4.学校团委接受了一项任务,完成这项任务的时间t与参加此项任务的同学人数x之间满足关系式:t=ax+bx.当x=10时,t=100,当x=20时,t=100.若想所用时间最短,则参加人数为( )
A.13 B.14
C.15 D.16
... ... ...
关键词:高中人教B版数学必修一PPT课件免费下载,章末复习提升课PPT下载,函数PPT下载,.PPT格式;