人教A版(2019)数学必修第二册《复数的三角表示》复数PPT
展开
《复数的三角表示》复数PPT
第一部分内容:学习目标
了解复数的三角形式,了解复数的代数表示与三角表示之间的关系
了解复数乘、除运算的三角表示及其几何意义
... ... ...
复数的三角表示PPT,第二部分内容:自主学习
问题导学
预习教材P83-P89的内容,思考以下问题:
1.复数z=a+bi的三角形式是什么?
2.复数的辐角、辐角的主值是什么?
3.复数三角形式的乘、除运算公式是什么?
4.复数三角形式乘、除运算的几何意义是什么?
新知初探
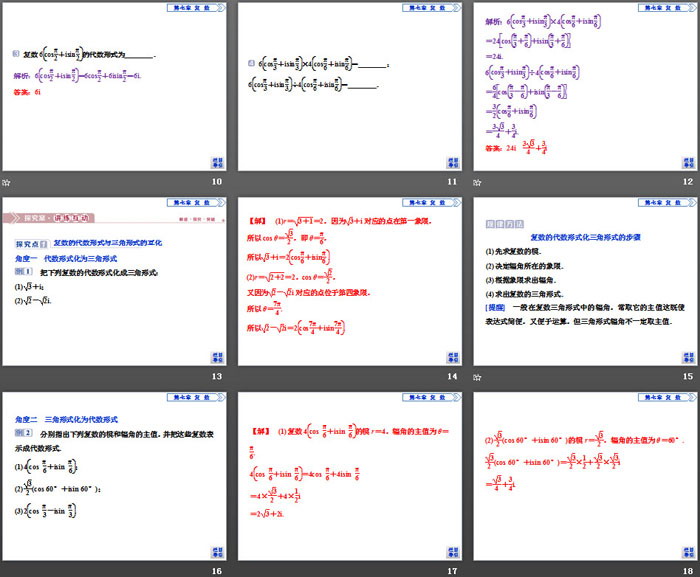
1.复数的三角表示式及复数的辐角和辐角的主值
一般地,任何一个复数z=a+bi都可以表示成r(cos θ+isin θ)的形式,其中,r是复数z的_____;θ是以x轴的非负半轴为始边,向量OZ→所在射线(射线OZ→)为终边的角,叫做复数z=a+bi的辐角,我们规定在0≤θ<2π范围内的辐角θ的值为辐角的主值,通常记作argz.r(cos θ+isin θ)叫做复数z=a+bi的三角表示式,简称三角形式.a+bi叫做复数的代数表示式,简称代数形式.
名师点拨
(1)任何一个不为零的复数的辐角有无限多个值,且这些值相差2π的整数倍.
(2)复数0的辐角是任意的.
(3)在0≤θ<2π范围内的辐角θ的值为辐角的主值,通常记作argz,且0≤argz<2π.
(4)两个非零复数相等当且仅当它们的模与辐角的主值分别相等.
2.复数三角形式的乘、除运算
若复数z1=r1(cos θ1+isin θ1),z2=r2(cos θ2+isin θ2),且z1≠z2,则
(1)z1z2=r1(cos θ1+isin θ1)•r2(cos θ2+isin θ2)
=______________________________.
(2)z1z2=r1(cos θ1+isin θ1)r2(cos θ2+isin θ2)
=______________________________.
即:两个复数相乘,积的模等于____________________,积的辐角等于各复数的辐角的_____.
两个复数相除,商的模等于__________的模除以__________的模所得的商,商的辐角等于__________的辐角减去__________的辐角所得的差.
... ... ...
复数的三角表示PPT,第三部分内容:自我检测
1.判断(正确的打“√”,错误的打“×”)
(1)复数的辐角是唯一的.( )
(2)z=cos θ-isin θ是复数的三角形式.( )
(3)z=-2(cos θ+isin θ)是复数的三角形式.( )
(4)复数z=cos π+isin π的模是1,辐角的主值是π.( )
2. 复数z=1+i的三角形式为z=________.
3. 复数6cosπ2+isinπ2的代数形式为________.
4. 6cosπ3+isinπ3×4cosπ6+isinπ6=________;
6cosπ3+isinπ3÷4cosπ6+isinπ6=________.
... ... ...
复数的三角表示PPT,第四部分内容:讲练互动
复数的代数形式与三角形式的互化
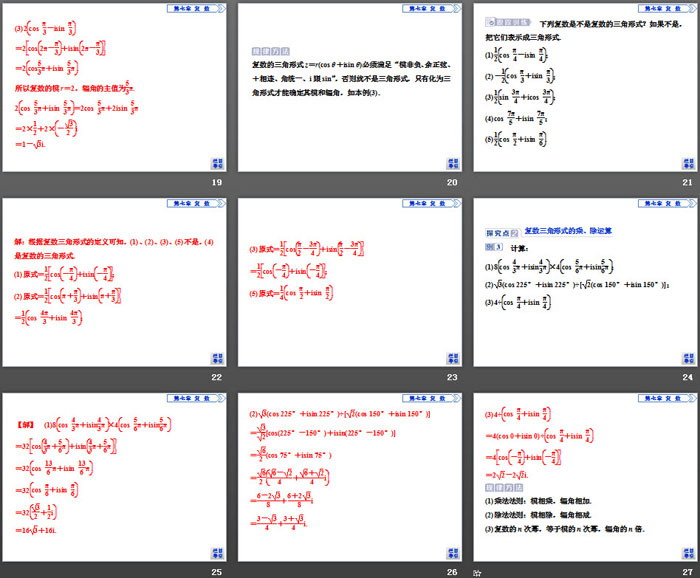
角度一 代数形式化为三角形式
把下列复数的代数形式化成三角形式:
(1)3+i;
(2)2-2i.
规律方法
复数的代数形式化三角形式的步骤
(1)先求复数的模.
(2)决定辐角所在的象限.
(3)根据象限求出辐角.
(4)求出复数的三角形式.
[提醒] 一般在复数三角形式中的辐角,常取它的主值这既使表达式简便,又便于运算,但三角形式辐角不一定取主值.
角度二 三角形式化为代数形式
分别指出下列复数的模和辐角的主值,并把这些复数表示成代数形式.
(1)4cos π6+isin π6;
(2)32(cos 60°+isin 60°);
(3)2cos π3-isin π3.
规律方法
复数的三角形式z=r(cos θ+isin θ)必须满足“模非负、余正弦、+相连、角统一、i跟sin”,否则就不是三角形式,只有化为三角形式才能确定其模和辐角,如本例(3).
... ... ...
复数的三角表示PPT,第五部分内容:达标反馈
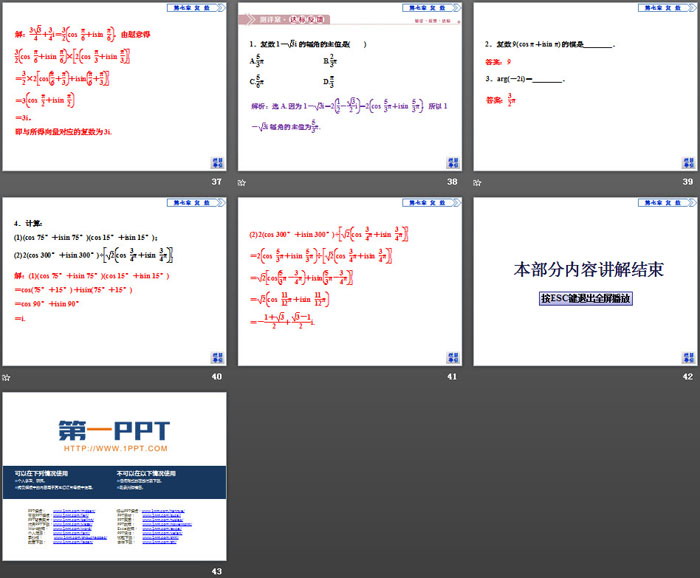
1.复数1-3i的辐角的主值是( )
A.53π B.23π
C.56π D.π3
2.复数9(cos π+isin π)的模是________.
3.arg(-2i)=________.
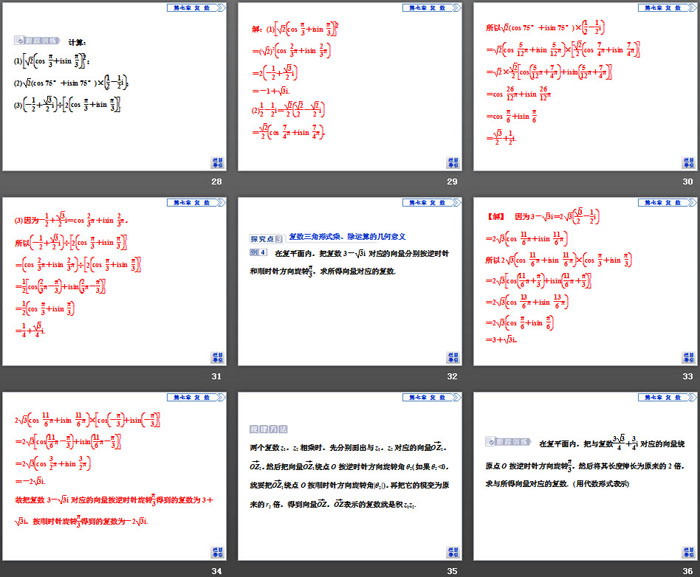
4.计算:
(1)(cos 75°+isin 75°)(cos 15°+isin 15°);
(2)2(cos 300°+isin 300°)÷2cos 34π+isin 34π.
关键词:高中人教A版数学必修二PPT课件免费下载,复数的三角表示PPT下载,复数PPT下载,.PPT格式;