冀教版(2012)数学八年级上册《等边三角形》PPT免费课件
展开
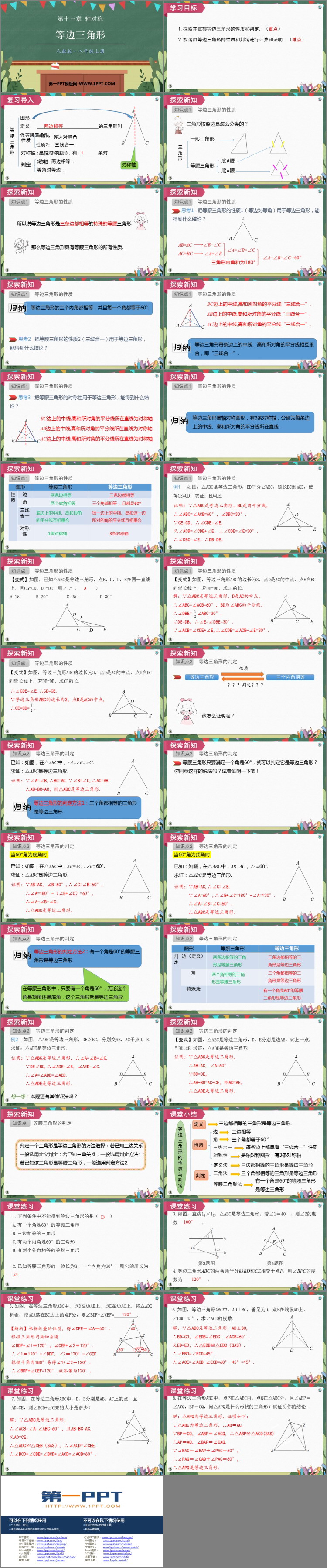
人教版八年级数学上册《等边三角形》PPT免费课件,共33页。
学习目标
1.探索并掌握等边三角形的性质和判定.(重点)
2.能运用等边三角形的性质和判定进行计算和证明.(难点)
探索新知
知识点1 等边三角形的性质
所以说等边三角形是三条边都相等的特殊的等腰三角形.
那么等边三角形具有等腰三角形的所有性质.
思考1 把等腰三角形的性质1(等边对等角)用于等边三角形,能得到什么结论?
等边三角形的三个内角都相等,并且每一个角都等于60°.
思考2 把等腰三角形的性质2(三线合一)用于等边三角形,能得到什么结论?
BC边上的中线,高和所对角的平分线“三线合一”.
AB边上的中线,高和所对角的平分线“三线合一”.
AC边上的中线,高和所对角的平分线“三线合一”.
等边三角形每条边上的中线、高和所对角的平分线相互重合,即“三线合一”.
思考3 把等腰三角形的对称性用于等边三角形,能得到什么结论?
BC边上的中线,高和所对角的平分线所在直线为对称轴.
AB边上的中线,高和所对角的平分线所在直线为对称轴.
AC边上的中线,高和所对角的平分线所在直线为对称轴.
知识点2 等边三角形的判定
已知:如图,在△ABC中,∠A=∠B=∠C.
求证:△ABC是等边三角形.
证明:∵∠A=∠B,∴BC=AC.∵∠B=∠C,∴AC=AB.
∴AB=BC=AC,则△ABC是等边三角形.
等边三角形的判定方法1:三个角都相等的三角形是等边三角形.
当60°角为底角时
已知:如图,在△ABC中,AB=AC,∠B=60°.
求证:△ABC是等边三角形.
证明:∵AB=AC,∠B=60°,∴∠C=∠B=60°.
∴∠A=180°-(∠B+∠C)=60°,
∴∠A=∠B=∠C.
∴△ABC是等边三角形.
等边三角形的判定方法2:有一个角是60°的等腰三角形是等边三角形.
在等腰三角形中,只要有一个角是60° ,无论这个角是顶角还是底角,这个三角形就是等边三角形.
... ... ...
关键词:等边三角形PPT课件免费下载,轴对称PPT下载,.PPTX格式;